오늘부터 자료구조에 대해서 자세하게 알아보는 시간을 가져보려고 한다. 앱의 효율성을 끌어올리기 위해서는 CS에 대한 이해가 뒷받침되어야 하기 때문에 총 6챕터로 나누어진 Swift 자료 구조 알고리즘의 자료를 한국어로 잘 번역해준 자료가 있어 이걸 통해 한번 공부해보자!
오늘은 전체 챕터를 한번 훑는 느낌으로 알아보도록 하자
복잡도 Complexity
우리가 구현하면서 혹은 코딩테스트를 풀면서 접하는 명칭 중 하나는 바로 복잡도이다. 이 복잡도는 소프트웨어 개발의 설계 단계에서 항상 묻게되는 질문이다.
아키텍처 관점에서 확장성은 앱을 변경하는 것이 얼마나 쉬운가를 다루는데 데이터 베이스 관점에서 확장성은 데이터베이스에서 데이터를 저장하고 검색하는 시간이다.
알고리즘에서 확장성은 인풋의 사이즈가 커질수록 알고리즘의 실행시간과 메모리 사용 측면에서 알고리즘이 수행하는 방식을 일컫는다.
적은 양의 데이터로 수행할 경우, 비싼 알고리즘은 빠르게 느껴질 수 있지만, 데이터의 양이 증가할 수록 비싼 알고리즘은 장애가 된다.
두번째 챕터에서는 Big O 표기법에 대해서 행시간과 메모리 사용량이라는 두 차원의 다른 확장성 레벨에서 살펴볼 것 이다.
시간 복잡도 Time Complexity
적은 양의 데이터에서는 아무리 무거운 알고리즘이더라도 요즘 하드웨어 속도로 인해 빠르게 작동하는 것으로 보일 수 있다. 하지만 데이터가 증가할 수록 무거운 알고리즘은 명백하게 효율성이 떨어지게 된다.
이 시간 복잡도는 인풋 사이즈가 증가할 수록 알고리즘을 실행하는데 걸리는 시간을 측정하는 것이다. 이번 섹션에서 가장 일반적인 시간 복잡도에 대해 알아보도록 하자.
- 상수 시간 Constant time
상수시간 알고리즘은 인풋의 사이즈와 상관없이 수행한 시간이 동일한 알고리즘을 뜻한다.
func checkFirst(names: [String]) {
if let first = names.first {
print(first)
} else {
print("no names"
}
}
여기서 names 배열의 사이즈는 이 함수 실행시간에 영향을 미치지 않는다. 인풋이 10이든 천만이든 이 함수는 오직 배열의 첫번째 요소만 검사하는 로직이기 때문이다.
이를 시각화 하면 이렇게 보여질 수 있다.
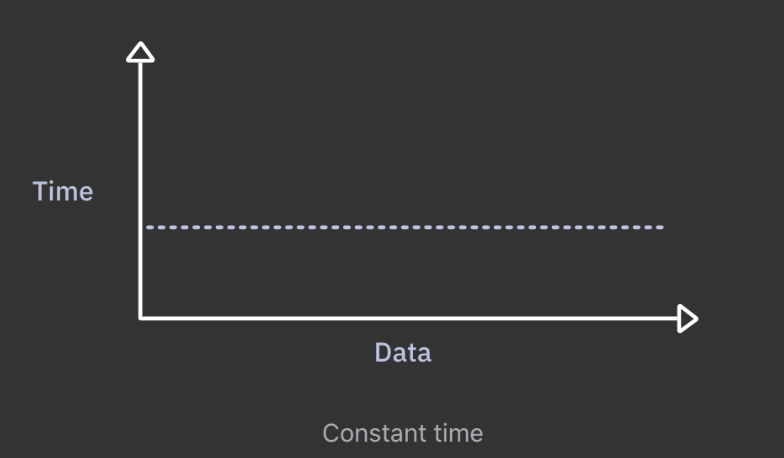
인풋 데이터가 증가해도 알고리즘이 수행하는 시간은 변하지 않는다. 간결함을 위해서 Bit O 표기법을 이용하여 다양한 규모의 시간복잡도를 나타내는데 이 상수시간의 Big O 표기법은 O(1) 이다
- 선형 시간 Linear time
func printNames(names: [String]) {
for name in names {
print(name)
}
}
이 함수는 String 배열 안에 있는 모든 이름을 출력한다. 인풋 배열의 사이즈가 증가할 수록 for 반복문의 반복 횟수도 같은 양으로 증가하게 되는데 이를 선형 시간 복잡도라고 한다.
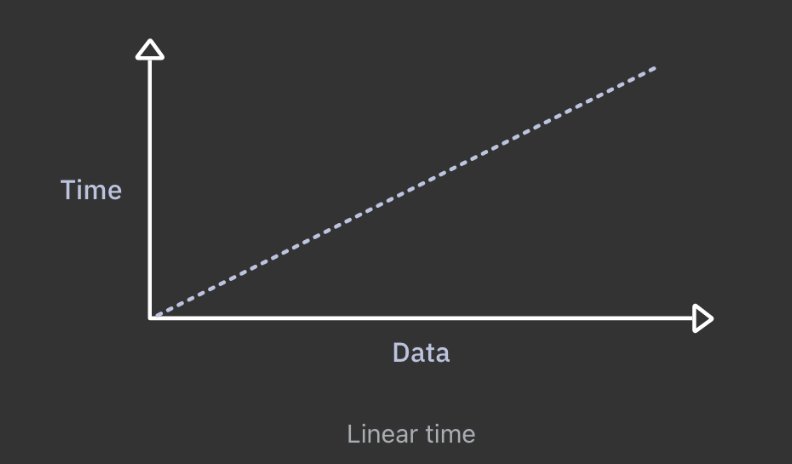
데이터의 양이 늘어나면 실행시간도 같은 양으로 늘어나는 형태인데 위에 선형 그래프는 Bit O 표기법으로 선형시간은 O(n) 이다.
** 그럼 여기서 궁금한 점 **
“모든 데이터에 대해 2개의 반복문이 있고 여섯개의 O(1) 메서드를 호출하는 함수는 O(2n + 6) 일까?”
시간 복잡도는 높은 수준의 성능 형태만 제공한다. 이 때문에 정해진 횟수만큼 반복되는 것은 계산에 포함되지 않는다. 모든 상수는 최종 Big O 표기법에서 삭제된다. 즉, O(2n+6) 은 O(n)과 동일하다.
- 평방시간(2차시간) Quadratic time
일반적으로는 n제곱이라고 하는 이 시간 복잡도는 인풋 사이즈의 제곱에 비례하는 시간이 걸린다. 아래 코드를 보면
func printNames(names: [String]) {
for _ in names {
for name in names {
print(name)
}
}
}
이번에는 함수가 배열에 있는 모든 이름 배열에 대한 이름을 출력하는데 만약 10개의 데이터가 있는 배열이라면 10개의 이름이 있는 전체 목록을 10번씩 출력한다. 총 100개의 출력문이 나오게 된다.
만약 인풋 사이즈가 하나 증가하면, 11개의 이름을 11번 출력하고 121개의 출력문이 나오게 된다. 선형시간 동안 수행되는 이전 함수와 다르게, n 제곱 알고리즘은 데이터 사이즈가 증가 할 수록 더 빠르게 과부화될 수 있다.
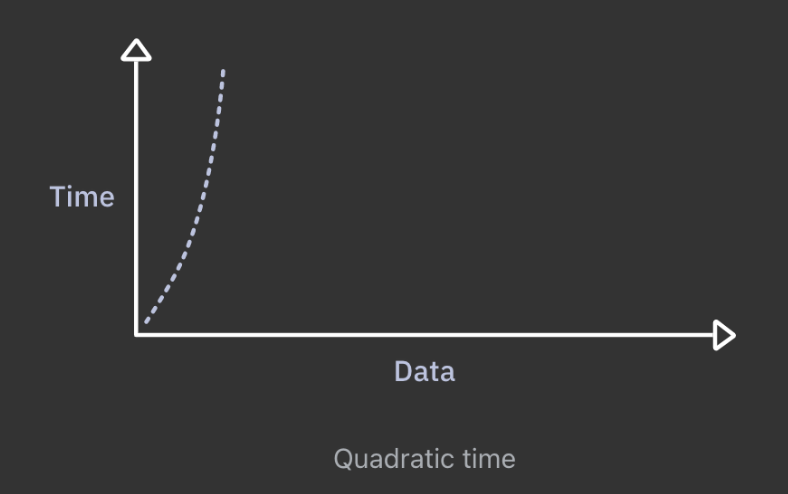
이미지에서 볼 수 있듯 인풋 데이터의 사이즈가 증가할 수록 알고리즘을 수행하는 시간은 급격하게 증가한다. 이 때문에 n 제곱 알고리즘은 규모에 따라서 수행되지는 않는다.
Big O 표기법으로 2차시간은 O(n2) 이다.
오늘은 간단하게 몇가지 복잡도에 대해서 알아봤다. 다음엔 추가적인 복잡도와 기초적인 자료구조에 대해서 알아 보도록 하자 🙂
오늘은 여기까지!
'◽️ Programming > ◽️ Computer Science' 카테고리의 다른 글
| iOS Swift의 자료 구조, 알고리즘에 대해서 알아보자 (3) (0) | 2024.11.04 |
|---|---|
| iOS Swift의 자료구조, 알고리즘에 대해서 알아보자 (2) (0) | 2024.10.30 |
| [CS] 컴퓨터 구조에 대해서 자세하게 알아보자 (1) | 2024.07.15 |
| [CS] 운영체제에 대해서 자세하게 알아보자 (0) | 2024.07.13 |
| 객체지향 프로그래밍과 SOLID원칙 (0) | 2024.06.24 |

